我々は、ワンステップ生成モデリングのための原理的かつ効果的なフレームワークを提案する。 フローマッチング法によってモデル化される瞬間速度とは対照的に、流れ場を特徴付ける平均速度の概念を導入する。平均速度と瞬間速度の間に明確に定義された恒等式が導出され、ニューラルネットワークの学習に用いられる。MeanFlowモデルと呼ばれる我々の手法は自己完結型であり、事前学習、蒸留、カリキュラム学習を必要としない。MeanFlowは強力な実験的性能を示し、ゼロから学習したImageNet 256×256における単一関数評価(1-NFE)で3.43のFIDを達成し、従来の最先端のワンステップ拡散/フローモデルを大幅に上回る性能を示した。本研究は、ワンステップ拡散/フローモデルとそのマルチステップ先行モデルとの間のギャップを大幅に縮めるものであり、これらの強力なモデルの基礎を再検討する将来の研究を促進することを期待する。
生成モデリングの目的は、事前分布をデータ分布に変換することです。フローマッチング[28, 2, 30]は、ある分布を別の分布に輸送するフローパスを構築するための直感的で概念的にシンプルなフレームワークを提供します。拡散モデル[42, 44, 19]と密接に関連するフローマッチングは、モデルの学習を導く速度場に焦点を当てています。導入以来、フローマッチングは現代の生成モデリングにおいて広く採用されています[11, 33, 35]。
フローマッチングモデルと拡散モデルはどちらも生成中に反復サンプリングを行う。最近の研究では、少数ステップ、特に1ステップのフィードフォワード生成モデルに大きな注目が集まっている。この分野の先駆者として、一貫性モデル[46, 43, 15, 31]は、同じパスに沿ってサンプリングされた入力に対するネットワーク出力に一貫性制約を導入する。有望な結果であるにもかかわらず、一貫性制約はネットワークの挙動の特性として課されるのに対し、学習を導くはずの根底にある真実の場の特性は依然として不明である。その結果、学習は不安定になる可能性があり、時間領域を徐々に制約するために慎重に設計された「離散化カリキュラム」[46, 43, 15]が必要となる。
本研究では、ワンステップ生成のための、原理的かつ効果的なフレームワーク「MeanFlow」を提案する。その核となるアイデアは、Flow Matchingで一般的にモデル化される瞬間速度とは対照的に、平均速度を表す新たな正解場を導入することである。平均速度は、変位と時間間隔の比として定義され、変位は瞬間速度の時間積分によって与えられる。この定義のみに基づいて、平均速度と瞬間速度の間に明確かつ本質的な関係を導出する。これは、ネットワーク学習を導くための原理的な基盤として自然に機能する。
この基本概念に基づき、ニューラルネットワークを訓練して平均速度場を直接モデル化する。ネットワークが平均速度と瞬間速度の間の固有の関係を満たすように促す損失関数を導入する。追加の一貫性ヒューリスティックは不要である。真のターゲット場の存在により、最適解は原理的に特定のネットワークに依存しないことが保証され、実際にはより堅牢で安定した訓練につながる。さらに、このフレームワークは分類器不要のガイダンス(CFG)[18]をターゲット場に自然に組み込むことができ、ガイダンス使用時のサンプリング時に追加コストが発生しないことを示す。
我々のMeanFlowモデルは、ワンステップ生成モデリングにおいて高い経験的性能を示している。ImageNet 256×256 [7]において、我々の手法は1-NFE(関数評価回数)生成を用いて3.43のFIDを達成した。この結果は、同クラスの先行研究における最先端手法を50%から70%の相対マージンで大幅に上回る(図1)。さらに、我々の手法は自己完結型の生成モデルであり、事前学習、蒸留、カリキュラム学習を必要とせず、完全にゼロから学習される。本研究は、ワンステップ拡散/フローモデルと、それらのマルチステップ先行研究との間のギャップを大きく埋めるものであり、これらの強力なモデルの基礎を再考するための将来の研究に刺激を与えることを期待している。

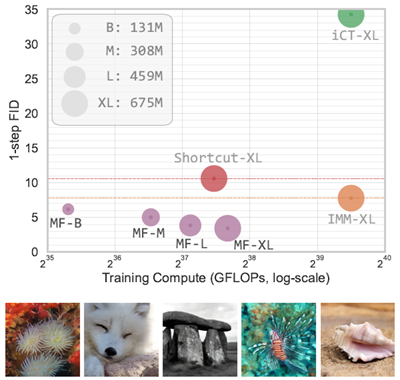
図1:ImageNetでの256×256のワンステップ生成。我々のMeanFlow(MF)モデルは、従来の最先端のワンステップ拡散/フロー法よりも大幅に優れた生成品質を実現している。ここで、iCT [43]、Shortcut [13]、そして我々のMFはすべて1-NFE生成であるのに対し、IMMの1ステップ結果[52]は2-NFEガイダンスを伴う。詳細な数値は表2に示している。表示されている画像は、我々の1-NFEモデルによって生成されたものである。
拡散とフローマッチング 過去10年間で、拡散モデル [42, 44, 19, 45] は、生成モデリングのための非常に成功したフレームワークへと発展してきました。これらのモデルは、クリーンなデータにノイズを徐々に追加し、ニューラルネットワークを学習させてこのプロセスを逆転させます。この手順では、確率微分方程式 (SDE) を解き、それを確率フロー常微分方程式 (ODE) [45, 22] として再定式化します。フローマッチング法 [28, 2, 30] は、分布間のフローパスを定義する速度場をモデル化することで、このフレームワークを拡張します。フローマッチングは、連続時間正規化フロー [36] の一種と見なすこともできます。
少ステップ拡散/フローモデル サンプリングステップの削減は、実践的および理論的な観点から重要な考慮事項となっている。一つのアプローチとして、事前学習済みの多ステップ拡散モデルを少ステップモデルに蒸留する手法(例えば、[39, 14, 41] やスコア蒸留 [32, 50, 53])が挙げられる。少ステップモデルの学習に関する初期の研究 [46] は、蒸留に基づく手法の進化に基づいている。一方、一貫性モデル [46] は、蒸留を必要としないスタンドアロンの生成モデルとして開発されている。これらのモデルは、異なる時間ステップにおけるネットワーク出力に一貫性制約を課し、軌跡に沿って同じエンドポイントを生成するように促す。様々な一貫性モデルと学習戦略 [46, 43, 15, 31, 49] が研究されてきた。
最近の研究では、拡散/フローベースの量を2つの時間依存変数に関して特徴付けることに焦点を置いた手法がいくつか提案されています。[3]では、フローマップは2つの時間ステップ間のフローの積分として定義され、学習用にいくつかの形式のマッチング損失が開発されています。本手法が基づいている平均速度と比較すると、フローマップは変位に対応します。ショートカットモデル[13]は、フローマッチングに加えて、異なる離散時間間隔におけるフロー間の関係を捉える自己無撞着損失関数を導入しています。誘導モーメントマッチング[52]は、異なる時間ステップにおける確率的補間の自己無撞着性をモデル化します。
フローマッチング [28, 30, 1] は、速度場によって表されるフローを、2つの確率分布間でマッチングさせることを学習する生成モデルの一種です。正式には、データ \(x ∼ p_{data}(x)\) と事前分布 \(ϵ ∼ p_{prior}(ϵ)\) が与えられた場合、時間 \(t\) を持つフローパス \(z_t = a_tx + b_tϵ\) を構築できます。ここで、\(a_t\) と bt は定義済みのスケジュールです。速度 \(v_t\) は \(v_t = z_t^\prime = a_t^\prime x + b_t^\prime ϵ\) と定義され、\({}^\prime\) は時間微分を表します。この速度は[28]において条件付き速度と呼ばれ、\(v_t = v_t(z_t | x)\)と表記される。 図2左を参照。一般的に用いられるスケジュールは\(a_t = 1 − t\)および\(b_t = t\)であり、\(v_t = ϵ − x\)となる。
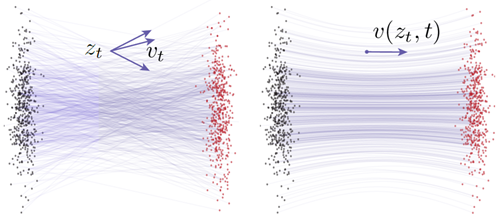
図2: フローマッチングにおける速度場 [28]。左: 条件付きフロー [28]。与えられた \(z_t\) は異なる \((x,\epsilon)\) ペアから発生する可能性があり、その結果、異なる条件付き速度 vt が生じる。右: 周辺フロー [28]。これは、すべての可能な条件付き速度を周辺化することで得られる。周辺速度場は、ネットワーク学習の基礎となる正解値場として機能する。ここで示されるすべての速度は、本質的に瞬間速度である。図は [12] に従う。(灰色の点: 事前分布からのサンプル、赤色の点: データからのサンプル。)
与えられた\(z_t\)とその\(v_t\)は異なる\(x\)と\(ϵ\)から生じる可能性があるため、フローマッチングは本質的に、限界速度[28]と呼ばれるすべての可能性に対する期待値をモデル化します(図2右)。 \[ v(z_t, t) ≜ \mathbb{E}_{p_t}(v_t|z_t)[v_t] \tag{1} \] ニューラルネットワーク \(v_θ\) は、\(θ\) によってパラメータ化され、限界速度場 \(\mathcal{L}_{FM}(θ) =\mathbb{E}_{t,p_t(z_t)}v_θ(z_t, t) − v(z_t, t)^2\) に適合するように学習される。式 (1) の限界化のため、この損失関数を計算することは不可能であるが、代わりに条件付きフローマッチング損失を評価することが提案されている。[28] : \(\mathbb{L}_{CFM}(θ) = \mathbb{E}_{t,x,ϵ}v_θ(z_t, t) − v_t(z_t | x)^2\)、ここで、目標 \(v_t\) は条件付き速度である。 \(\mathcal{L}_{CFM}\)を最小化することは\(\mathcal{L}_{FM}\)を最小化することと同義である[28]。
限界速度場 \(v(z_t, t)\) が与えられた場合、サンプルは \(z_t\) の ODE を解くことによって生成されます。 \[ \frac{d}{dt}z_t = v(z_t, t) \tag{2} \] \(z_1 = ϵ ∼ p_{prior}\) から開始します。解は次のように書けます: \(z_r = z_t −\int_r^t v(z_τ , τ )dτ\)。ここで、r は別の時間ステップを表します。実際には、この積分は離散時間ステップにわたって数値的に近似されます。たとえば、1 階の常微分方程式ソルバーであるオイラー法は、各ステップを次のように計算します: \(z_{t_{i+1}} = z_{t_i} + (t_{i+1} − t_i)v(z_{t_i} , t_i)\)。高階ソルバーも適用できます。
条件付き流れが直線(「整流化」)となるように設計されている場合でも[28, 30]、限界速度場(式(1))は典型的には曲線軌道を誘起することは注目に値する。図2に説明を示す。また、この非直線性はニューラルネットワーク近似の結果だけではなく、基礎となる真の限界速度場から生じていることも強調しておく。曲線軌道に粗い離散化を適用すると、数値常微分方程式ソルバーは不正確な結果をもたらす。
私たちのアプローチの核となるアイデアは、平均速度を表す新しい場を導入することです。一方、Flow Matchingでモデル化された速度は瞬間速度を表します。
平均速度 平均速度は、2つの時間ステップ \(t\) と \(r\) の間の変位(積分によって得られる)を時間間隔で割ったものと定義します。正式には、平均速度uは次のように表されます。 \[ u(z_t, r, t) ≜ \frac{1}{t − r}\int_r^t v(z_τ , τ )dτ \tag{3} \] 概念上の違いを強調するため、本稿では平均速度をu、瞬間速度をvと表記する。\(u(z_t, r, t)\) は \((r, t)\) に共に依存する場である。\(u\) の場は図3に示されている。一般に、平均速度uは瞬間速度 \(v\) の関数の結果である。つまり、\(u = \mathcal{F}[v] ≜ \frac{1}{t−r}\int_r^t vdτ\)である。これはvによって誘起される場であり、ニューラルネットワークには依存しない。概念的には、瞬間速度vがFlow Matchingにおける真の値場として機能するのと同様に、本稿における平均速度uは学習のための基礎となる真の値場を提供する。

図3: 平均速度場 \(u(z, r, t)\)。左端:瞬間速度 \(v\) は経路の接線方向を決定しますが、式(3)で定義される平均速度 \(u(z, r, t)\) は、通常、v と一致しません。平均速度は変位と一致し、\((t − r)u(z, r, t)\) となります。右の3つのサブプロット:場 \(u(z, r, t)\) は \(r\) と \(t\) の両方に依存し、ここでは \(t =\) 0.5、0.7、1.0 の場合を示しています。
定義により、u 体は特定の境界条件と「無矛盾性」制約を満たす([46] の用語を一般化する)。\(r→t\) のとき、\(\lim_{r→t} u = v\) が成立する。さらに、ある種の「無矛盾性」が自然に満たされる。つまり、[r, t] 上で 1 つの大きなステップを取ることは、任意の中間時刻 s において、\([r, s]\) と \([s, t]\) 上で 2 つの小さな連続したステップを取ることと「無矛盾」である。これを理解するには、\((t − r)u(z_t, r, t) = (s − r)u(z_s, r, s) + (t − s)u(z_t, s, t)\) という式に注目してください。これは、積分の加法性から直接導かれます。 \(\int_r^t vdτ =\int_r^s vdτ +\int_s^t vdτ\)。したがって、真の u を正確に近似するネットワークは、明示的な制約を必要とせずに、本質的に整合性関係を満たすことが期待されます。
MeanFlowモデルの最終的な目的は、ニューラルネットワーク\(u_θ(z_t, r, t)\)を用いて平均速度を近似することです。この方法には、この量を正確に近似できれば、\(u_θ(ϵ, 0, 1)\)の1回の評価でフローパス全体を近似できるという大きな利点があります。言い換えれば、また実験的にも示すように、このアプローチは、瞬間速度をモデル化する際に必要だった推論時に時間積分を明示的に近似する必要がないため、単一または少数ステップの生成に適しています。しかし、式(3)で定義された平均速度をネットワークの学習に正解として直接使用することは、学習中に積分を評価する必要があるため、扱いにくいです。私たちの重要な洞察は、平均速度の定義式を操作することで、瞬間速度しかアクセスできない場合でも、最終的に学習に適した最適化ターゲットを構築できるということです。
MeanFlow恒等式 訓練に適した定式化とするために、式(3)を次のように書き直します。 \[ (t − r)u(z_t, r, t) = \int_r^t v(z_τ , τ )dτ \tag{4} \] ここで、\(r\) は \(t\) に依存しないとして、両辺を \(t\) について微分します。すると、次の式が得られます。 \[ \frac{d}{dt}(t − r)u(z_t, r, t) =\frac{d}{dt}\int_r^t v(z_τ , τ )dτ ⇒ u(z_t, r, t) + (t − r) \frac{d}{dt}u(z_t, r, t) = v(z_t, t) \tag{5} \] ここで、左辺の操作には積の定理を用い、右辺には微積分学の基本定理2を用いる。項を整理すると、次の恒等式が得られる。
2 \(r\)が\(t\)に依存する場合、ライプニッツの定理[26]によれば\(\frac{d}{dt}\int_r^t v(z_τ, τ)dτ = v(z_t, t) − v(z_r, r)\frac{dr}{dt}\)となります。
\[ \underbrace{u(z_t, r, t)}_{平均速度}= \underbrace{v(z_t, t)}_{瞬間速度.} −(t − r)\underbrace{\frac{d}{dt}u(z_t, r, t)}_{時間微分} \tag{6} \] この式を「MeanFlow 恒等式」と呼びます。これは、\(v\) と \(u\) の関係を記述するものです。 式 (6) と式 (4) が同値であることは簡単に示せます(付録 B.3 を参照)。
式(6)の右辺は\(u(z_t, r, t)\)の「ターゲット」形式を提供しており、これを利用してニューラルネットワークを学習するための損失関数を構築します。適切なターゲットとして機能するためには、時間微分項をさらに分解する必要があり、これについては次に説明します。
時間微分の計算 式(6)の\(\frac{d}{dt}u\)項を計算する際、\(\frac{d}{dt}\)は全微分を表し、偏微分で展開できることに注意してください。 \[ \frac{d}{dt}u(z_t, r, t) =\frac{dz_t}{dt}∂_zu +\frac{dr}{dt}∂_ru +\frac{dt}{dt}∂_tu \tag{7} \] \(\frac{dz_t}{dt} = v(z_t, t)\) (式(2)参照)、\(\frac{dr}{dt} = 0\)、\(\frac{dt}{dt} = 1\)のとき、\(u\)と\(v\)の間には別の関係があります。 \[ \frac{d}{dt}u(z_t, r, t) = v(z_t, t)∂_zu + ∂_tu \tag{8} \] この式は、全微分が、\([∂_zu, ∂_ru, ∂_tu]\)(関数uのヤコビ行列)と接ベクトル\([v, 0, 1]\)との間のヤコビベクトル積(JVP)によって与えられることを示しています。最近のライブラリでは、これはPyTorchのtorch.func.jvpやJAXのjax.jvpなどのjvpインターフェースによって効率的に計算できます(JAXについては後述します)。
平均速度を用いた学習ここまでの定式化は、ネットワークパラメータ化に依存しません。ここで、\(u\) を学習するモデルを導入します。正式には、ネットワーク \(u_θ\) をパラメータ化し、MeanFlow 恒等式 (式(6)) を満たすように促します。具体的には、この目的関数を最小化します。 \[ \begin{align} \mathcal{L}(θ) &= \mathbb{E}||u_θ(z_t, r, t) − sg(u_{tgt})||_2^2 \tag{9} \\ \\ ここで u_{tgt} &= v(z_t, t) − (t − r) (v(z_t, t)∂_zu_θ + ∂_tu_θ) \tag{10} \end{align} \] 項 \(u_{tgt}\) は、式(6) によって決定される有効な回帰ターゲットとして機能します。このターゲットは、瞬間速度 \(v\) を唯一の正解信号として使用し、積分計算は不要です。ターゲットには \(u\) の微分 (つまり \(∂u\)) が含まれる必要がありますが、それらはパラメーター化された対応するもの (つまり \(∂_{u_θ}\)) に置き換えられます。損失関数では、一般的な手法 [46, 43, 15, 31, 13] に従って、ターゲット \(u_{tgt}\) に stop-gradient (sg) 演算が適用されます。このケースでは、ヤコビアンベクトル積を介した「二重逆伝播」が不要になり、高階最適化を回避できます。最適化のためのこれらの実践にもかかわらず、uθがゼロ損失を達成する場合、それがMeanFlow恒等式(式(6))を満たし、したがって元の定義(式(3))を満たすことが簡単に示せます。
式(10)の速度\(v(z_t, t)\)はFlow Matching[28]における限界速度である(図2右参照)。[28]に従ってこれを条件付き速度に置き換える(図2左)。これにより目標値は以下のようになる。 \[ u_{tgt} = v_t − (t − r)\left(v_t∂_zu_θ + ∂_tu_θ\right) \tag{11} \] \(v_t = a_t^\prime x + b_t^\prime \epsilon\) は条件付き速度 [28] であり、デフォルトでは \(v_t = \epsilon − x\) であることを思い出してください。
損失関数式(9)を最小化する擬似コードをアルゴリズム1に示す。全体として、本手法は概念的に単純であり、Flow Matchingと同様に動作するが、主な違いは、マッチング対象が平均速度の考慮により \(−(t−r) (v_t∂_zu_θ + ∂_tu_θ)\) によって変更される点である。特に、条件 \(t = r\) に制限すると、第2項が消滅し、本手法は標準的なFlow Matchingと完全に一致することに留意されたい。
アルゴリズム1では、jvp演算は非常に効率的です。 本質的には、jvpによる\(\frac{d}{dt}u\)の計算には、ニューラルネットワークにおける標準的なバックプロパゲーションと同様に、1回のバックワードパスのみが必要です。\(\frac{d}{dt}u\)はターゲットutgtの一部であり、したがってstopgradの影響を受けるため(\(θ\)に関して)、ニューラルネットワーク最適化のためのバックプロパゲーション(\(θ\)に関して)では\(\frac{d}{dt}u\)を定数として扱い、高階勾配計算は発生しません。 したがって、jvpは1回の余分なバックワードパスのみを導入し、そのコストはバックプロパゲーションと同程度です。アルゴリズム1のJAX実装では、オーバーヘッドは総トレーニング時間の20%未満です(付録を参照)。

サンプリング MeanFlowモデルを用いたサンプリングは、時間積分を平均速度に置き換えるだけで実行されます。 \[ z_r = z_t − (t − r)u(z_t, r, t) \tag{12} \] 1ステップサンプリングの場合、\(z_0 = z_1 − u(z_1, 0, 1)\) と単純に書けます。ただし、\(z_1 =\epsilon ∼ p_{prior}(\epsilon)\) です。 アルゴリズム2に擬似コードを示します。本研究では1ステップサンプリングが主な焦点ですが、この式を用いれば数ステップサンプリングも簡単に実行できることを強調しておきます。

先行研究との関連 従来のワンステップ生成モデル [46, 43, 15, 31, 49, 23, 13, 52] と関連しながらも、本手法はより原理的な枠組みを提供する。本手法の中核は、2つの基礎場 \(v\) と \(u\) 間の関数的関係であり、これは自然に u が満たすべき MeanFlow 恒等式 (式 (6)) につながる。この恒等式はニューラルネットワークの導入に依存しない。対照的に、先行研究は通常、ニューラルネットワークの挙動に課される追加の一貫性制約に依存している。一貫性モデル [46, 43, 15, 31] は、データ側にアンカーされたパスに焦点を当てている。我々の表記法では、これは任意の t に対して \(r ≡ 0\) を固定することに相当する。結果として、一貫性モデルは、我々のモデルとは異なり、単一の時間変数を条件とする。一方、Shortcut [13] モデルと IMM [52] モデルは2つの時間変数を条件としており、追加の2時間自己無撞着制約を導入する。対照的に、本手法は平均速度の定義のみに基づいており、学習に用いる MeanFlow 恒等式(式(6))はこの定義から自然に導かれ、追加の仮定は存在しない。
我々の手法は、分類器不要ガイダンス(CFG)[18]を自然にサポートする。サンプリング時にCFGを単純に適用するとNFEが2倍になるが、我々はCFGを基礎となる正解場の特性として扱う。この定式化により、サンプリング中の1-NFEの挙動を維持しながら、CFGの利点を享受することができる。
正解場 新しい正解場 \(v^{cfg}\) を構築します。 \[ v^{cfg}(z_t, t | c) ≜ ω v(z_t, t | c) + (1 − ω) v(z_t, t) \tag{13} \] これはクラス条件場とクラス無条件場の線形結合です。 \[ v(z_t, t | \mathbf{c}) ≜ \mathbb{E}_{p_t}(v_t|z_t,\mathbf{c})[v_t] and v(z_t, t) ≜ \mathbb{E}_c[v(z_t, t | c)] \tag{14} \] ここで、\(v_t\)は条件付き速度[28](より正確には、この文脈ではサンプル条件付き速度)である。 MeanFlowの精神に従い、\(v^{cfg}\)に対応する平均速度\(u^{cfg}\)を導入する。 MeanFlow恒等式(式(6))によれば、\(u^{cfg}\)は以下を満たす。 \[ u^{cfg}(z_t, r, t | \mathbf{c}) = v^{cfg}(z_t, t | \mathbf{c}) − (t − r) \frac{d}{dt}u^{cfg}(z_t, r, t | \mathbf{c}) \tag{15} \] ここでも、\(v^{cfg}\) と \(u^{cfg}\) はニューラルネットワークに依存しない基礎的な正解場です。ここで、式(13)で定義されている\(v^{cfg}\) は次のように書き直すことができます。 \[ v^{cfg}(z_t, t | \mathbf{c}) = ω v(z_t, t | \mathbf{c}) + (1 − ω) u^{cfg}(z_t, t, t) \tag{16} \] ここでは関係3: \(v(z_t, t) = v^{cfg}(z_t, t)\)、および \(v^{cfg}(z_t, t) = u^{cfg}(z_t, t, t)\) を活用します。
3 次の式に注目してください: \(v^{cfg}(z_t, t) ≜ \mathbb{E}_c[v^{cfg}(z_t, t | \mathbf{c})] = ω \mathbb{E}_c[v(z_t, t | \mathbf{c})]+(1−ω) v(z_t, t) = v(z_t, t)\).
ガイダンス付き学習 式(15)と式(16)を用いて、ネットワークとその学習目標を構築する。 \(u^{cfg}\)を関数\(u_θ^{cfg}\)によって直接パラメータ化する。式(15)に基づいて、目的関数は以下の通りとなる。 \[ \begin{align} \mathcal{L}(θ) &= \mathbb{E}||u_θ^{cfg}(z_t, r, t | \mathbf{c}) − sg(u^{tgt})||_2^2 \tag{17} \\ \\ where u^{tgt} &= \tilde{v}_t − (t − r)\left(\tilde{v}_t∂_zu_θ^{cfg} + ∂_tu_θ^{cfg}\right) \tag{18} \end{align} \] この定式化は式(9)に似ていますが、唯一の違いは修正された\(\tilde{v}_t\)を持つ点です。 \[ \tilde{v}_t ≜ ω v_t + (1 − ω) u_θ^{cfg} (z_t, t, t) \tag{19} \] これは式(16)によって駆動される。式(16)の限界速度である\(v(z_t, t | \mathbf{c})\)の項は、[28]に従って(サンプル)条件付き速度vtに置き換えられる。\(ω = 1\)の場合には、この損失関数は式(9)のCFGなしの場合に退化する。
式(17)のネットワーク\(u_θ^{cfg}\)をクラス無条件入力にさらすために、[18]に従って、10%の確率でクラス条件を削除します。同様の動機から、式(19)の\(u_θ^{cfg} (z_t, t, t)\)をクラス無条件バージョンとクラス条件付きバージョンの両方にさらすこともできます。詳細は付録B.1を参照してください。
CFGを用いた単一NFEサンプリング 我々の定式化では、\(u_θ^{cfg}\) は、CFG速度 \(v^{cfg}\) によって誘起される平均速度 \(u^{cfg}\) を直接モデル化します(式(13))。その結果、サンプリング中に線形結合は不要になります。つまり、単一のNFEのみを使用したワンステップサンプリング(アルゴリズム2を参照)には、\(u_θ^{cfg}\) を直接使用します。 この定式化は、望ましい単一NFEの挙動を維持します。
損失メトリクス 式(9)で考慮されているメトリクスはL2損失の2乗である。[46, 43, 15]に従って、様々な損失メトリクスを検討する。一般に、損失関数は\(\mathcal{L} = ‖Δ‖_2^{2γ}‖)の形で考慮される。 ここで、‖Δ‖は回帰誤差を表す。\(‖Δ‖_2^{2γ}‖)を最小化することは、適応損失重みを用いてL2損失の2乗\(‖Δ‖_2^2‖)を最小化することと等価であることが証明されている([15]を参照)。詳細は付録を参照。実際には、重みを \(w = 1/(Δ_2^2+ c)^p\) と設定します。ここで、\(p = 1 − γ\) かつ \(c > 0\) (例えば、\(10^{−3}\)) です。適応的に重み付けされた損失は \(sg(w)·\mathcal{L}\) であり、\(\mathcal{L} = ∥Δ_2^2\) です。\(p = 0.5\) の場合、これは [43] の Pseudo-Huber 損失に類似します。実験では異なる p 値を比較します。
サンプリング時間ステップ \((r, t)\)。 定義済みの分布から2つの時間ステップ \((r, t)\) をサンプリングします。 2種類の分布を調査します。(i) 一様分布 \(\mathcal{U}(0, 1)\)、および (ii) ロジット正規分布 [11] です。ロジット正規分布では、まず正規分布 \(\mathcal{N}(μ, σ)\) からサンプルが抽出され、次にロジスティック関数を用いて \((0, 1)\) にマッピングされます。サンプリングされたペアが与えられた場合、大きい方の値を \(t\) に、小さい方の値を \(r\) に割り当てます。\(r = t\) となるランダムサンプルを一定の割合で設定します。
\((r, t)\) に関する条件付け 時間変数を符号化するために位置埋め込み [48] を使用し、これらを組み合わせてニューラルネットワークの条件付けとして提供します。場は \(u_θ(z_t, r, t)\) でパラメータ化されますが、ネットワークが \((r, t)\) を直接条件付ける必要はありません。 例えば、\(Δt = t − r\) として、ネットワークが \((t,Δt)\) を直接条件付けることができます。この場合、\(u_θ(·, r, t) ≜ net(·, t, t − r)\) となり、net はネットワークです。JVP 計算は常に関数 \(u_θ(·, r, t)\) に関して行われます。実験では、さまざまな形式の条件付けを比較します。
実験設定。主要な実験はImageNet [7] を用いて256×256の解像度で生成する。5万枚の生成画像に対してFréchet Inception Distance (FID) [17] を評価する。関数評価回数(NFE)を検証し、デフォルトで1-NFE生成を研究する。[34, 13, 52] に従い、事前学習済みVAEトークナイザー [37] の潜在空間上にモデルを実装する。256×256画像の場合、トークナイザーは32×32×4の潜在空間を生成し、これがモデルへの入力となる。モデルはすべてゼロから学習した。実装の詳細は付録Aを参照。アブレーション研究では、[34] で開発されたViT-B/4アーキテクチャ(つまり、パッチサイズが4の「ベース」サイズ)[9] を使用し、80エポック(40万回の反復)学習を行った。参考までに、[34]のDiT-B/4は68.4 FID、SiT-B/4 [33](我々の再現)は58.9 FIDであり、どちらも250-NFEサンプリングを使用している。
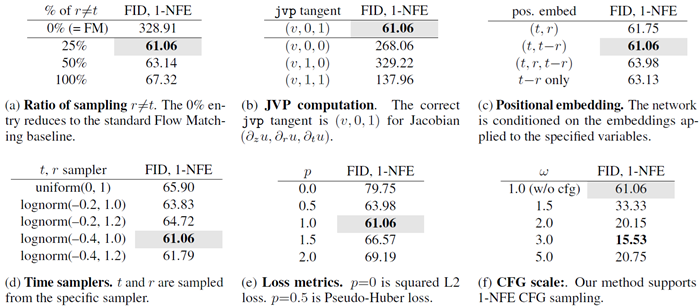
表1: 1-NFE ImageNet 256×256世代におけるアブレーション研究。FID-50Kが評価対象。デフォルト設定は灰色でマーク:B/4バックボーン、80エポックのゼロからの学習。
表1のモデル特性を調査し、次に分析します。 Flow MatchingからMean Flowsへ。本手法は、修正されたターゲット(アルゴリズム1)を持つFlow Matchingと見なすことができ、\(r\)が常に\(t\)に等しい場合、標準的なFlow Matchingに縮約されます。表1aは、\(r \neq t\)をランダムにサンプリングする比率を比較しています。\(r \neq t\)の比率が0%の場合(Flow Matchingに縮約)、1-NFE生成において妥当な結果が得られません。\(r \neq t\)の比率が0以外の場合、MeanFlowが有効になり、1-NFE生成において意味のある結果が得られます。モデルは、瞬間速度\((r = t)\)の学習と、修正されたターゲットを介して\(r \neq t\)への伝播の間でバランスをとっていることがわかります。ここで、最適な FID は 25% の比率で達成され、100% の比率でも有効な結果が得られます。
JVP 計算 JVP 演算式 (8) は、すべての \((r, t)\) 座標を結び付ける中核的な関係として機能します。表 1b では、意図的に誤った JVP 計算を実行する破壊的比較を行っています。これは、JVP 計算が正しい場合にのみ意味のある結果が得られることを示しています。特に、\(∂_zu\) に沿った JVP 接線は d 次元であり、\(d\) はデータ次元 (ここでは 32×32×4) です。一方、\(∂_ru\) と \(∂_tu\) に沿った接線は 1 次元です。それでも、これら 2 つの時間変数は場 \(u\) を決定するため、たとえ 1 次元であっても、その役割は重要です。
\((r, t)\) の条件付け 4.3節で述べたように、\(u_θ(z, r, t)\) は様々な形式の明示的な位置埋め込みによって表すことができます。例えば、\(u_θ(·, r, t) ≜ net(·, t, t − r)\) です。表1cはこれらのバリエーションを比較しています。表1cは、検討した \((r, t)\) 埋め込みのすべてのバリエーションが意味のある1-NFE結果をもたらし、フレームワークとしてのMeanFlowの有効性を実証していることを示しています。\((t, t − r)\)、つまり時間と間隔を埋め込むと最良の結果が得られますが、\((r, t)\) を直接埋め込むとほぼ同様の結果が得られます。特に、区間 \(t − r\) のみを埋め込んでも妥当な結果が得られます。
時間サンプラー 先行研究 [11] では、t をサンプリングするために使用される分布が生成品質に影響を与えることが示されている。表 1d では、\((r, t)\) をサンプリングするために使用される分布を調べる。\((r, t)\) は最初に独立にサンプリングされ、その後、スワップによって \(t > r\) を強制する後処理ステップが実行され、\(r \neq t\) の割合が指定された比率に制限される点に注意されたい。表 1d は、ロジット正規サンプラーが最良のパフォーマンスを発揮することを報告しており、これは Flow Matching [11] の観察と一致している。
損失メトリクス 損失メトリクスの選択は、数ステップ/1ステップ生成の性能に大きく影響することが報告されている[43]。この側面を表1eで考察する。我々の損失メトリクスは、べき乗p(第4.3節)を用いた適応的損失重み付け[15]によって実装されている。表1eは、\(p = 1\)が最良の結果を達成する一方で、\(p = 0.5\)(擬似Huber損失[43]に類似)も競争力のある性能を示すことを示している。標準の2乗L2損失(ここでは\(p = 0\))は他の設定と比較して性能が劣るが、それでも[43]の観察と一致して有意義な結果を生成する。
ガイダンススケール 表1fはCFGを用いた結果を示しています。多段階生成における観察結果[34]と一致して、CFGは1-NFE設定でも生成品質を大幅に向上させます。私たちのCFG定式化(4.2節)は、1-NFEサンプリングを自然にサポートすることを強調します。
スケーラビリティ 図4は、より大きなモデルサイズと異なる学習期間におけるMeanFlowの1-NFE FID結果を示しています。Transformerベースの拡散/フローモデル(DiT [34]およびSiT [33])の挙動と一致して、MeanFlowモデルは1-NFE生成において有望なスケーラビリティを示しています。
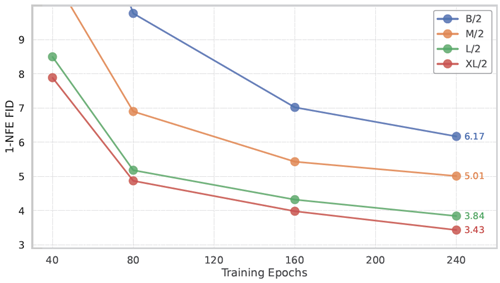
図4:ImageNet 256×256におけるMeanFlowモデルのスケーラビリティ。1-NFE生成FIDが報告されています。すべてのモデルはゼロから学習されています。CFGは1-NFEサンプリング動作を維持しながら適用されています。本手法は、モデルサイズに関して有望なスケーラビリティを示しています。
ImageNet 256×256の比較。図1では、表2(左)にまとめられている従来の1ステップ拡散/フローモデルと比較しています。全体的に、MeanFlowは同クラスの従来の手法を大きく上回っています。MeanFlowは3.43 FIDを達成しており、これはIMMの1ステップ結果7.77 [52] と比較して50%以上の相対的改善です。1-NFE(1ステップだけでなく)生成のみを比較すると、MeanFlowは従来の最先端技術(10.60、Shortcut [13])と比較して約70%の相対的改善を示しています。私たちの手法は、1ステップ拡散/フローモデルと多ステップ拡散/フローモデル間のギャップを大きく埋めます。
2段階NFE生成において、本手法はFID 2.20を達成した(表2、左下)。この結果は、多段階拡散/フローモデルの代表的なベースライン、すなわちDiT [34](FID 2.27)およびSiT [33](FID 2.15)と同等であり、どちらも同じXL/2バックボーンに基づくNFEは250×2である(表2、右)。本結果は、少段階拡散/フローモデルが多段階拡散/フローモデルに匹敵することを示唆している。REPA [51]などの直交改良法も適用可能であり、これは今後の課題である。
特筆すべきは、我々の手法が自己完結型であり、完全にゼロから学習されていることです。事前学習、蒸留、あるいは[43, 15, 31]で採用されたカリキュラム学習を一切行わずに、優れた結果を達成しています。
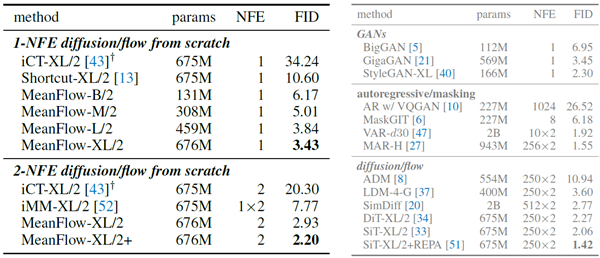
表2:ImageNet-256×256におけるクラス条件付き生成。該当する場合、すべてのエントリはCFGを用いて報告されています。左:ゼロから学習した1-NFEおよび2-NFE拡散/フローモデル。右:参考として他の生成モデルファミリー。両方の表で「×2」は、CFGではサンプリングステップごとにNFEが2になることを示しています。MeanFlowモデルはすべて240エポックで学習されていますが、「MeanFlow-XL+」はより多くのエポックで学習され、付録に記載されているより長い学習用に選択された構成で学習されています。†:iCT [43]の結果は[52]によって報告されています。
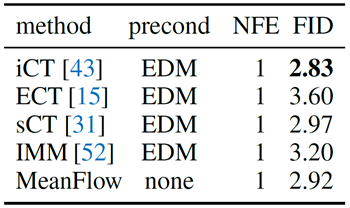
CIFAR-10との比較。表3に、CIFAR-10 [25] (32×32) における無条件生成結果を示す。FID-50Kは1-NFEサンプリングで報告されている。すべてのエントリは、[44] (約55M) から開発された同じU-net [38] をピクセル空間に直接適用したものである。他の競合手法はすべてEDMスタイルの前処理器 [22] を使用しているのに対し、本手法は前処理器を使用していない。実装の詳細は付録を参照。このデータセットにおいて、本手法は従来の手法と競合可能である。
我々は、ワンステップ生成のための原理的かつ効果的なフレームワークであるMeanFlowを紹介しました。大まかに言えば、本研究で検討するシナリオは、物理学におけるマルチスケールシミュレーション問題に関連しており、空間または時間において、様々なスケール、長さ、解像度を伴う場合があります。数値シミュレーションの実行は、コンピュータが様々なスケールを解像する能力によって本質的に制限されます。我々の定式化は、基礎となる量を粗い粒度レベルで記述することを伴っており、これは物理学における多くの重要な応用の根底にある共通のテーマです。我々の研究が、関連分野における生成モデリング、シミュレーション、および力学システムの研究との橋渡しとなることを願っています。
TPUへのアクセスを許可してくださったGoogle TPU Research Cloud(TRC)に深く感謝いたします。Zhengyang Gengは、Bosch Center for AIからの資金提供の一部を受けています。Zico Kolterは、Boschによるラボへの資金提供に深く感謝いたします。Mingyang DengとXingjian Baiは、MIT-IBM Watson AI Labの助成金の一部を受けています。JAXとTPUの実装にご協力いただいたRunqian Wang、Qiao Sun、Zhicheng Jiang、Hanhong Zhao、Yiyang Lu、Xianbang Wangに感謝いたします。
ImageNet 256×256。潜在表現の抽出には標準的なVAEトークナイザーを使用する。4 潜在表現のサイズは32×32×4で、これがモデルへの入力となる。バックボーンアーキテクチャはDiT [34]に準拠しており、DiTはViT [9]をベースにadaLN-Zero [34]を用いて条件付けを行っている。2つの時間変数(例えば(r, t))を条件付けするには、各時間変数に位置埋め込みを適用し、その後2層MLPを適用して合計する。DiTアーキテクチャブロックはそのまま残し、アーキテクチャの改善は直交かつ可能である。構成の詳細は表4に示す。
4 https://huggingface.co/pcuenq/sd-vae-ft-mse-flax
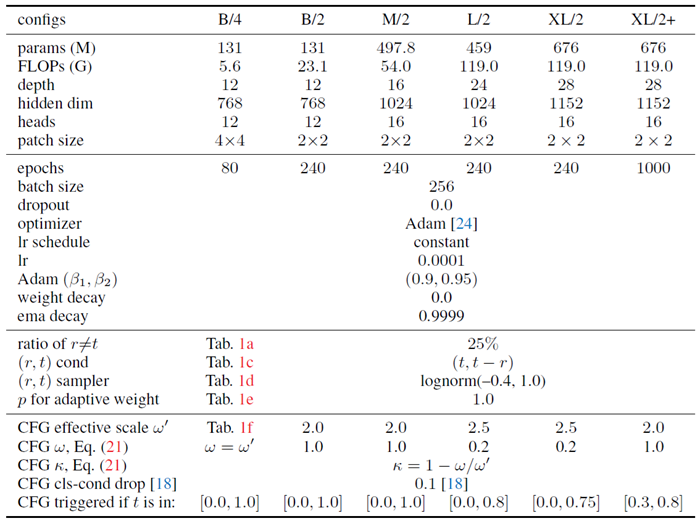
表4: ImageNet 256×256での構成。B/4は私たちのアブレーションモデルです。
CIFAR-10 CIFAR-10上でクラス無条件生成の実験を行う。実装は標準的なFlow Matchingの手法[29]に従う。モデルへの入力はピクセル空間で32×32×3である。ネットワークは[44] (∼55M) から開発されたU-net [38]であり、これは比較対象となる他のベースラインでも一般的に使用されている。2つの時間変数(ここでは\((t, t − r)\))に位置埋め込みを適用し、それらを連結して条件付けを行う。EDM前処理[22]は使用しない。
Adamを用い、学習率0.0006、バッチサイズ1024、((β_1, β_2) = (0.9, 0.999))、ドロップアウト0.2、重み減衰0、EMA減衰0.99995とする。モデルは80万回反復学習し(ウォームアップ1万回を含む)、[16]で評価した。((r, t))サンプラーはlognorm(-2.0, 2.0)である。サンプリング比(r \neq t)は75%である。適応重み付けの検出力(p)は0.75である。データ拡張の設定は[22]に従い、垂直反転と回転は無効である。
4.2節では、我々の手法をCFGをサポートするように自然に拡張する方法について議論した。必要な唯一の変更は、式(19)を用いてターゲットを修正することである。式(19)には、クラス無条件の \(u^{cfg}\) のみが与えられていることがわかる。オリジナルのCFG [18]では、クラス条件付き予測とクラス無条件予測を混合し、ランダムドロップ法でアプローチするのが標準的な方法である。同様の考え方が我々の回帰ターゲットにも適用できることが分かる。
正式には、混合スケール\(κ\)を導入し、式(16)を次のように書き直す。 \[ v^{cfg}(z_t, t | \mathbf{c}) = ω v(z_t, t | \mathbf{c}) + κ u^{cfg}(z_t, t, t | \mathbf{c}) + (1−ω−κ) u^{cfg}(z_t, t, t) \tag{20} \] ここで、κ の役割は、右辺で \(u^{cfg}( · | \mathbf{c})\) と混合することです。式 (20) は、式 (16) を導出する際に使用した関係 \(v(z_t, t) = v^{cfg}(z_t, t)\) および \(v^{cfg}(z_t, t) = u^{cfg}(z_t, t, t)\) を利用することで、実効誘導スケール \(ω^\prime = \frac{ω}{1−κ}\) を持つ元の CFG 定式化 (式 (13)) を満たすことが示せます。 これにより、式 (19) は次のように書き直されます。 \[ \tilde{v}_t ≜ ω\underbrace{(\epsilon − x)}_{sample\; v_t} + \underbrace{κu_θ^{cfg} (z_t, t, t | \mathbf{c}) }_{クラス条件出力} + \underbrace{(1−ω−κ) u_θ^{cfg}(z_t, t, t)}_{クラス無条件出力} \tag{21} \] 損失関数は式(17)で定義されたものと同じである。
κ導入の影響は表5に示されている。ここでは、実効誘導スケール \(ω^\prime\) を2.0に固定し、\(κ\) を変化させている。これは、\(κ\) による混合によって発電品質がさらに向上することを示す。ただし、本論文の表1fにおけるアブレーションではこの改善は考慮されておらず、\(κ\) は0に設定されていることに注意されたい。
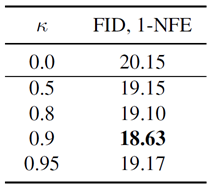
表5: MeanFlowの改良CFG。\(κ\)は式(20)で定義され、その目的はクラス条件付き\(u^{cfg}(·|\mathbf{c})\)とクラス無条件\(u^{cfg}(·)\)の両方がターゲットに現れるようにすることである。この表では、\(ω^\prime\)(\(ω^\prime = ω/(1 − κ)\)で与えられる)を2.0に固定する。したがって、異なる\(κ\)値に対して、\(ω\)を\(ω = (1−κ)·ω^\prime\)に設定する。\(κ = 0\)の場合、式(19)のCFGの場合にフォールバックする(表1fも参照)。標準的なCFGのクラス条件をランダムに削除する手法[18]と同様に、クラス条件付きucfgとクラス無条件ucfgをターゲットに混在させることで生成品質が向上することがわかりました。
L2損失の2乗は\(\mathcal{L} = ‖Δ‖_2^2\)で与えられ、\(Δ = u_θ − u^{tgt}\)は回帰誤差を表す。 一般的に、べき乗L2損失\(\mathcal{L}_γ = ‖Δ‖_2^{2γ}\)を採用することができる。ここで、\(γ\)はユーザーが指定したハイパーパラメータである。 この損失を最小化することは、適応的に重み付けされたL2損失の2乗を最小化することと同等である。 ([15]を参照): \(\frac{d}{dθ}\mathcal{L}_γ = γ(‖Δ‖_2^2)^{(γ−1)} ·\frac{d‖Δ‖_2^2}{dθ}\)。これは、L2損失の2乗 \((‖Δ‖_2^2)\) を損失適応型重み \(λ ∝ ‖Δ‖_2^{2(γ−1)}\) で重み付けしていると考えることができる。実際には、[15] に従って、次のように重み付けする。 \[ w = 1/(∥Δ∥_2^2+ c)^p \tag{22} \] ここで、\(p = 1 − γ\) および \(c > 0\) はゼロ除算を避けるための小さな定数です。\(p = 0.5\) の場合、これは [43] の擬似Huber損失に類似します。適応的に重み付けされた損失は \(sg(w) ·\mathcal{L}\) であり、sg は停止勾配演算子を表します。
本論文では、定義式(4)から出発して、MeanFlow恒等式(6)を導出した。これは、「式(4)⇒式(6)」、すなわち式(6)が式(4)の必要条件であることを示す。 次に、それが十分条件でもあることを示す。すなわち、「式(6)⇒式(4)」である。
一般に、微分が等しいことは積分が等しいことを意味しません。定数分だけ異なる場合もあります。 ここでは、定数分が打ち消されることを示します。「変位場」S を次のように書き表すとします。 \[ S(z_t, r, t) = (t − r)u(z_t, r, t) \tag{23} \] \(S\) を任意関数として扱うと、一般に、導関数の等式は、ある定数を除けば、積分の等式にのみ帰着する。 \[ \frac{d}{dt}S(z_t, r, t) = v(z_t, t) ⇒ S(z_t, r, t) + C_1 =\int_r^t v(z_τ , τ )dτ + C_2 \tag{24} \] しかし、Sの定義では\(S|_{t=r} = 0\)となり、また\(t = r\)のとき\(\int_r^t vdτ = 0\)となり、\(C_1 = C_2\)となります。これは「式(6) ⇒ 式(4)」を示しています。
この十分性は、変位 \(S\) を直接モデル化するのではなく、平均速度 \(u\) をモデル化することによる結果であることに注意してください。変位の微分値の等式、例えば \(\frac{d}{dt}S = v\) を強制しても、自動的に \(S =\int_r^t vdτ\) が得られるわけではありません。\(S\) を直接パラメータ化すると、追加の境界条件 \(S|_{t=r} = 0\) が必要になります。この定式化は、この条件を自動的に満たします。
JVP計算はいくつかの手法では懸念事項となる場合がありますが、本手法では非常に軽量です。本手法では、計算された積(ヤコビ行列と接線ベクトルの積)は停止勾配(式(10))の影響を受けるため、\(θ\)に対するバックプロパゲーションを用いてSGDを実行する際には定数として扱われます。したがって、\(θ\)バックプロパゲーションにオーバーヘッドは追加されません。
したがって、この積を計算することで発生する追加の計算は、jvp演算によって実行される「後方」パスです。この後方パスは、ニューラルネットワークの最適化に使用される標準的な後方パス(\(θ\)に関して)に類似しています。実際、JAX [4]などの一部の深層学習ライブラリでは、標準的なバックプロパゲーション(\(θ\)に関して)を計算するために同様のインターフェースを使用しています。私たちのケースでは、パラメータ\(θ\)ではなく入力変数へのバックプロパゲーションのみが必要なため、標準的なバックプロパゲーションよりもさらにコストが低くなります。このオーバーヘッドは小さいです。
アブレーションモデルB/4において、JVPによるオーバーヘッドをベンチマークしました。モデルはJAXで実装し、v4-8 TPUでベンチマークを行いました。MeanFlowをFlow Matchingと比較すると、JVPによるバックワードパスのみがオーバーヘッドとなります。JVPのフォワードパスは標準的なフォワードプロパゲーションであり、Flow Matching(または一般的な目的関数)でも同様に実行する必要があることに注意してください。ベンチマークでは、Flow Matchingを使用した場合のトレーニングコストは0.045秒/イテレータ、MeanFlowを使用した場合のトレーニングコストは0.052秒/イテレータで、ウォールクロックオーバーヘッドはわずか16%です。
図5は、1-NFEモデルを使用したImageNet 256×256でのキュレーション生成例を示しています。

図5:1-NFE生成結果。1-NFEモデル(MeanFlow-XL/2、3.43 FID)を用いたImageNet 256×256におけるクラス条件付き生成のキュレーション例を示します。